
The Matrix Library
The scientific computing matrix library (SCMAT) is designed around a set of matrix abstractions that permit very general matrix implementations. This flexibility is needed to support diverse computing environments. For example, this library must support, at a minimum: simple matrices that provide efficient matrix computations in a uniprocessor environment, clusters of processors with enough memory to store all matrices connected by a relatively slow network (workstations on an LAN), clusters of processors with enough memory to store all matrices and a fast interconnect network (a massively parallel machine such as the Intel Paragon), and clusters of machines that don't have enough memory to hold entire matrices.
- Overview
- Matrix Dimensions
- Matrix Reference Classes
- Abstract Matrix Classes
- Matrix Storage
- Manipulating Matrix Elements with Element Operations
- SCElementOp Specializations
- Local Matrices
- Replicated Matrices
- Distributed Matrices
- Blocked Matrices
Overview
The design of SCMAT differs from other object-oriented matrix packages in two important ways. First, the matrix classes are abstract base classes. No storage layout is defined and virtual function calls must be used to access individual matrix elements. This would have a negative performance impact if users needed to frequently access matrix elements. The interface to the matrix classes is hopefully rich enough to avoid individual matrix element access for any computationally significant task. The second major difference is that symmetric matrices do not inherit from matrices, etc. The SCMAT user must know whether a matrix is symmetric at all places it is used if any performance gain, by virtue of symmetry, is expected.
Dimension information is contained objects of the SCDimension type. In addition to the simple integer dimension, application specific blocking information can be provided. For example, in a quantum chemistry application, the dimension corresponding to the atomic orbital basis set will have block sizes that correspond to the shells. Dimensions are used to create new matrix or vector objects.
The primary abstract classes are SCMatrix, SymmSCMatrix, DiagSCMatrix, and SCVector. These represent matrices, symmetric matrices, diagonal matrices, and vectors, respectively. These abstract classes are specialized into groups of classes. For example, the locally stored matrix implementation specializes the abstract classes to LocalSCMatrix, LocalSymmSCMatrix, LocalDiagSCMatrix, LocalSCVector, LocalSCDimension, and LocalSCMatrixKit. These specializations are all designed to work with each other. However, a given specialization is incompatible with other matrix specializations. An attempt to multiply a local matrix by a distributed matrix would generate an error at runtime.
Since the different groups of classes do not interoperate, some mechanism of creating consistent specializations is needed. This is done with SCMatrixKit objects. SCMatrixKit is an abstract base type which has specializations that correspond to each group of the matrix specializations. It is used to create matrices and vectors from that group. For example, the DistSCMatrixKit is used to create objects of type DistSCMatrix, DistSymmSCMatrix, DistDiagSCMatrix, and DistSCVector.
The abstract matrix classes and their derivations are usually not directly used by SCMAT users. The most convenient classes to use are the smart pointer classes RefSCMatrix, RefSymmSCMatrix, RefDiagSCMatrix, and RefSCDimension. These classes respectively inherit from Ref<SCMatrix>, Ref<SymmSCMatrix>, Ref<DiagSCMatrix>, and Ref<SCDimension>, providing automatic memory management through reference counting. The smart pointer classes also have matrix operations such as operator *(), operator-(), and operator+() defined as members for convenience. These forward the operations to the contained matrix object. The smart pointer classes also simplify creation of matrices by providing constructors that take as arguments one or more RefSCDimension's and a Ref<SCMatrixKit>. These initialize the smart pointer to contain a new matrix with a specialization corresponding to that of the Ref<SCMatrixKit>. Matrix operations not provided by the smart pointer classes but present as member in the abstract classes can be accessed with operator->().
If a needed matrix operation is missing, mechanisms exist to add more general operations. Operations which only depend on individual elements of matrices can be provided by specializations of the SCElementOp class. Sometimes we need operations on matrices with identical dimensions that examine each element in one matrix along with the corresponding element from the other matrix. This is accomplished with SCElementOp2 for two matrices and with SCElementOp3 for three.
Other features of SCMAT include run-time type facilities and persistence. Castdown operations (type conversions from less to more derived objects) and other run-time type information are provided by the DescribedClass base class. Persistence is not provided by inheriting from SavableState base clase as is the case with many other classes in the SC class hierarchies, because it is necessary to save objects in an implementation independent manner. If a calculation checkpoints a matrix on a single processor machine and later is restarted on a multiprocessor machine the matrix would need to be restored as a different matrix specialization. This is handled by saving and restoring matrices' and vectors' data without reference to the specialization.
The following include files are provided by the matrix library:
matrix.h- Usually, this is the only include file needed by users of matrices. It declares reference counting pointers to abstract matrices.
If kit for a matrix must be created, or a member specific to an implementation is needed, then that implementation's header file must be included.
elemop.h- This is the next most useful include file. It defines useful SCElementOp, SCElementOp2, and SCElementOp3 specializations.
abstract.h- This include file contains the declarations for abstract classes that users do not usually need to see. These include SCDimension, SCMatrix, SymmSCMatrix, DiagSCMatrix, SCMatrixKit. This file is currently included by matrix.h.
block.h- This file declares SCMatrixBlock and specializations. It only need be include by users implementing new SCElementOp specializations.
blkiter.h- This include file declares the implementations of SCMatrixBlockIter. It only need be include by users implementing new SCElementOp specializations.
vector3.h- This declares SCVector3, a lightweight vector of length three.
matrix3.h- This declares SCMatrix3, a lightweight matrix of dimension three by three. It includes vector3.h.
local.h- This include file is the matrix implementation for locally stored matrices. These are suitable for use in a uniprocessor environment. The LocalSCMatrixKit is the default matrix implementation returned by the static member SCMatrixKit::default_matrixkit. This file usually doesn't need to be included.
dist.h- This include file is the matrix implementation for distributed matrices. These are suitable for use in a distributed memory multiprocessor which does not have enough memory to hold all of the matrix elements on each processor. This file usually doesn't need to be included.
repl.h- This include file is the matrix implementation for replicated matrices. These are suitable for use in a distributed memory multiprocessor which does have enough memory to hold all of the matrix elements on each processor. This file usually doesn't need to be included.
blocked.h- This include file is the matrix implementation for blocked matrices. Blocked matrices store a matrix as subblocks that are matrices from another matrix specialization. These are used to save storage and computation time in quantum chemistry applications for molecules with other than
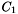 point group symmetry.
point group symmetry.
In addition to the simple integer dimension, objects of the SCDimension class contain application specific blocking information. This information is held in an object of class SCBlockInfo.
The easiest way to use SCMAT is through the smart pointer classes RefSCMatrix, RefSymmSCMatrix, RefDiagSCMatrix, RefSCVector, RefSCDimension, and Ref<SCMatrixKit>. These are based on the Ref reference counting package and automatically delete matrix objects when they are no longer needed. These reference classes also have common operations defined as members for convenience. This makes it unnecessary to also use the sometimes awkward syntax of operator->() to manipulate the contained objects.
This section documents the primary abstract classes: SCMatrix, SymmSCMatrix, DiagSCMatrix, and SCVector, as well as the SCMatrixKit class which allows the programmer to generate consistent specializations of matrices. These represent matrices, symmetric matrices, diagonal matrices, and vectors, respectively.
This section is primarily for implementers of new specializations of matrices. Users of existing matrices will be most interested in the matrix reference classes.
All elements of matrices and vectors are kept in blocks. The choice of blocks and where they are keep is left up to each matrix specialization.
Manipulating Matrix Elements with Element Operations
The SCElementOp, SCElementOp2, and SCElementOp3 classes can be used to maniupulate matrix elements.
Several commonly needed element operations are already coded up and available by including math/scmat/elemop.h. Below are descriptions of these classes:
- SCElementScalarProduct
- This SCElementOp2 computes the scalar product of two matrices or vectors. The result is available after the operation from the return value of the result() member.
- SCDestructiveElementProduct
- This SCElementOp2 replaces the elements of the matrix or vector whose element_op member is called. The resulting values are the element by element products of the two matrices or vectors.
- SCElementScale
- This scales each element by an amount given in the constructor.
- SCElementRandomize
- This generates random elements.
- SCElementAssign
- Assign to each element the value passed to the constructor.
- SCElementSquareRoot
- Replace each element with its square root.
- SCElementInvert
- Replace each element by its reciprocal.
- SCElementScaleDiagonal
- Scales the diagonal elements of a matrix by the argument passed to the constructor. Use of this on a vector is undefined.
- SCElementShiftDiagonal
- Add the value passed to the constructor to the diagonal elements of the matrix. Use of this on a vector is undefined.
- SCElementMaxAbs
- Find the maximum absolute value element in a matrix or vector. The result is available as the return value of the
result()member. - SCElementDot
- The constructor for this class takes three arguments: SCElementDot(double**a, double**b, int length). The length of each vector given by a and b is given by length. The number of vectors in a is the number of rows in the matrix and the number in b is the number of columns. To each element in the matrix
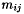 the dot product of the
the dot product of the 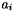 and
and 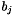 is added.
is added. - SCElementAccumulateSCMatrix
- This is obsolete---do not use it.
- SCElementAccumulateSymmSCMatrix
- This is obsolete---do not use it.
- SCElementAccumulateDiagSCMatrix
- This is obsolete---do not use it.
- SCElementAccumulateSCVector
- This is obsolete---do not use it.
Local matrices do no communication. All elements reside on each node and all computations are duplicated on each node.
Replicated matrices hold all of the elements on each node, however do some communications in order to reduce computation time.
Distributed matrices spread the elements across all the nodes and thus require less storage than local matrices however these use more communications than replicated matrices.
Blocked matrices are used to implement point group symmetry. Another matrix specialization is used to hold the diagonal subblocks of a matrix. The offdiagonal subblocks are known to be zero and not stored. This results in considerable savings in storage and computation for those cases where it applies.
Generated at Fri Jan 10 08:14:10 2003 for MPQC 2.1.3 using the documentation package Doxygen 1.2.14.